A neural architecture for Bayesian compressive sensing over the simplex via Laplace techniques
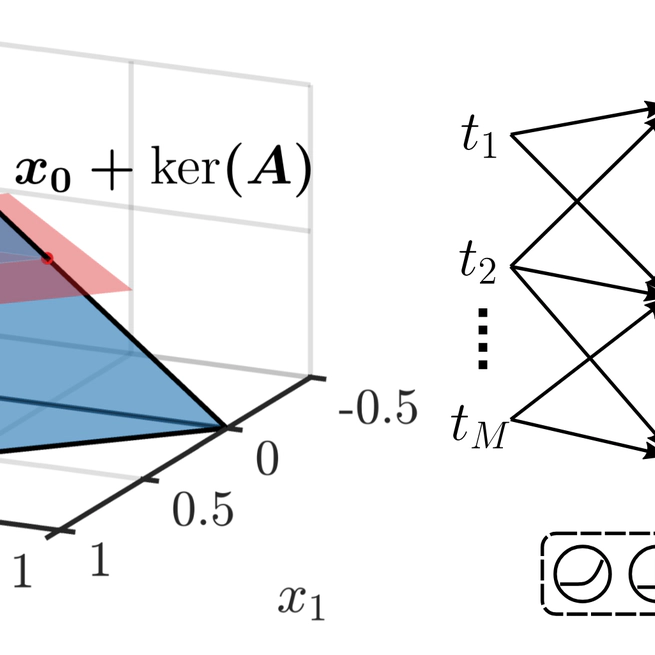
This paper introduces a novel theoretical and conceptual framework for designing neural architectures specifically for Bayesian compressive sensing of simplex-constrained sparse stochastic vectors. The core idea involves reframing the MMSE estimation problem as computing the centroid of a polytope, which is the intersection of a simplex and an affine subspace defined by compressive measurements. Leveraging multidimensional Laplace techniques, the authors derive a closed-form solution for this centroid computation and demonstrate how to directly map this solution to a neural network architecture composed of threshold, ReLU, and rectified polynomial activation functions. This unique construction results in an architecture where the number of layers equals the number of measurements, offering faster solutions in low-measurement scenarios and exhibiting robustness to small model mismatches. Simulations further indicate that this proposed architecture achieves superior approximations with fewer parameters compared to standard ReLU networks in supervised learning contexts.
Oct 2, 2018
Towards optimal nonlinearities for sparse recovery using higher-order statistics
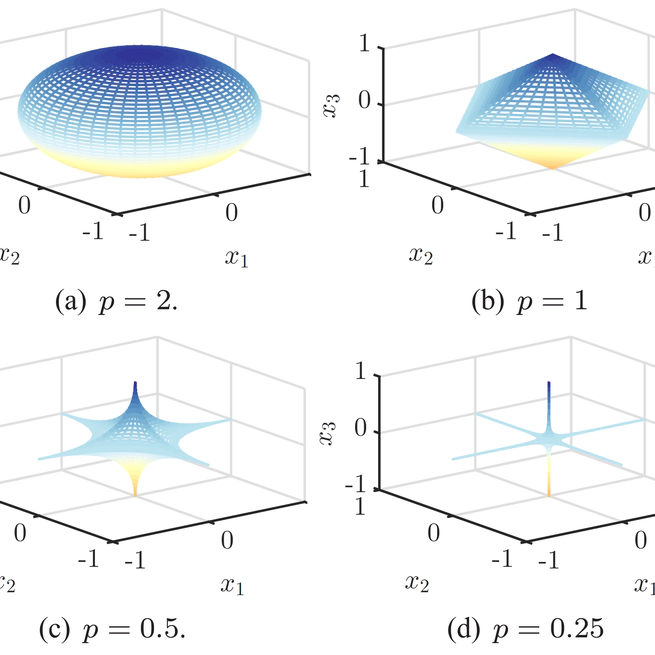
This paper investigates machine learning techniques to achieve low-latency approximate solutions for inverse problems, specifically focusing on recovering sparse stochastic signals within lp-balls using a probabilistic framework. The authors analyze the Bayesian mean-square-error (MSE) for two estimators. a linear one, and a structured nonlinear one comprising a linear operator followed by a Cartesian product of univariate nonlinear mappings. Crucially, the proposed nonlinear estimator maintains comparable complexity to its linear counterpart due to the efficient hardware implementation of the nonlinear mapping via look-up tables (LUTs). This structure is well-suited for neural networks and single-iterate shrinkage/thresholding algorithms, and an alternating minimization technique yields optimized operators and mappings that converge in MSE, making it highly appealing for real-time applications where traditional iterative optimization is infeasible.
Sep 5, 2016
A simple algorithm for approximation by nomographic functions
This paper presents a new algorithm for approximating multivariate functions using nomographic functions, which consist of a one-dimensional continuous and monotone outer function applied to a sum of univariate continuous inner functions. The core of the method involves solving a cone-constrained Rayleigh-Quotient optimization problem, drawing upon Analysis of Variance (ANOVA) for dimension-wise function decomposition and optimization over monotone polynomials. The utility of this algorithm is demonstrated through an example showcasing its application in distributed function computation over multiple-access channels.
Jul 13, 2015