Neural-ANOVA: Analytical Model Decomposition using Automatic Integration
The analysis of variance (ANOVA) decomposition offers a systematic method to understand the interaction effects that contribute to a specific decision output. In this paper we introduce Neural-ANOVA, an approach to decompose neural networks into the sum of lower-order models using the functional ANOVA decomposition. Our approach formulates a learning problem, which enables fast analytical evaluation of integrals over subspaces that appear in the calculation of the ANOVA decomposition. Finally, we conduct numerical experiments to provide insights into the approximation properties compared to other regression approaches from the literature.
Jul 31, 2024
Physics-informed neural networks for pathloss prediction
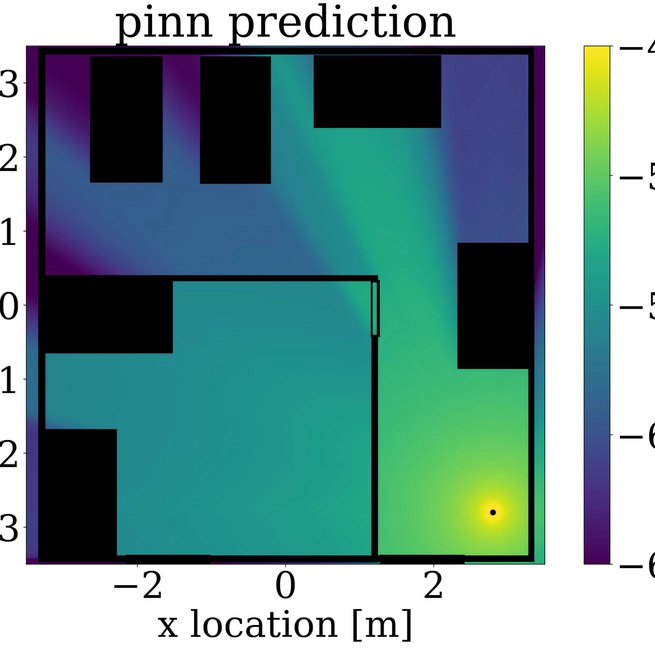
This paper presents a novel physics-informed machine learning method for pathloss prediction that significantly enhances generalization and prediction accuracy. The approach uniquely integrates both the inherent physical relationships within the spatial loss field and empirical pathloss measurements directly into the neural network's training process. This dual-constraint learning problem enables the model to achieve superior performance with fewer layers and parameters, resulting in exceptionally fast inference times crucial for subsequent applications like localization. Furthermore, the physics-informed framework substantially reduces the need for extensive training data, making this method highly adaptable and practical for diverse real-world pathloss prediction challenges.
Dec 14, 2023