A neural architecture for Bayesian compressive sensing over the simplex via Laplace techniques

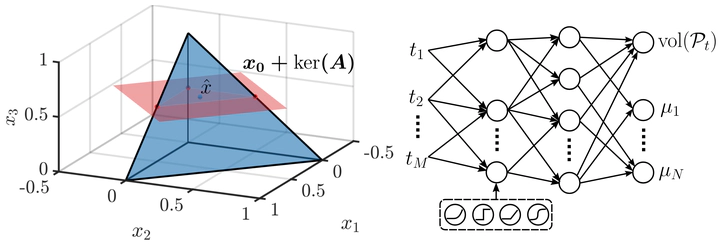
This paper introduces a novel theoretical and conceptual framework for designing neural architectures specifically for Bayesian compressive sensing of simplex-constrained sparse stochastic vectors. The core idea involves reframing the MMSE estimation problem as computing the centroid of a polytope, which is the intersection of a simplex and an affine subspace defined by compressive measurements. Leveraging multidimensional Laplace techniques, the authors derive a closed-form solution for this centroid computation and demonstrate how to directly map this solution to a neural network architecture composed of threshold, ReLU, and rectified polynomial activation functions. This unique construction results in an architecture where the number of layers equals the number of measurements, offering faster solutions in low-measurement scenarios and exhibiting robustness to small model mismatches. Simulations further indicate that this proposed architecture achieves superior approximations with fewer parameters compared to standard ReLU networks in supervised learning contexts.