A simple algorithm for approximation by nomographic functions

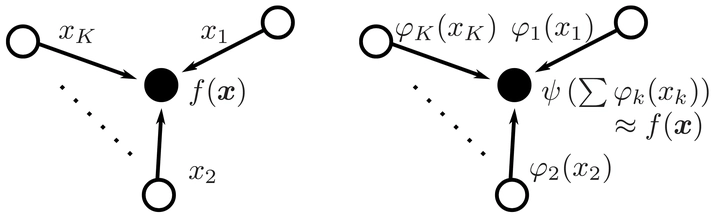
This paper presents a new algorithm for approximating multivariate functions using nomographic functions, which consist of a one-dimensional continuous and monotone outer function applied to a sum of univariate continuous inner functions. The core of the method involves solving a cone-constrained Rayleigh-Quotient optimization problem, drawing upon Analysis of Variance (ANOVA) for dimension-wise function decomposition and optimization over monotone polynomials. The utility of this algorithm is demonstrated through an example showcasing its application in distributed function computation over multiple-access channels.