Neural networks for integral equations and engineering applications @ The Alan Turing Institute

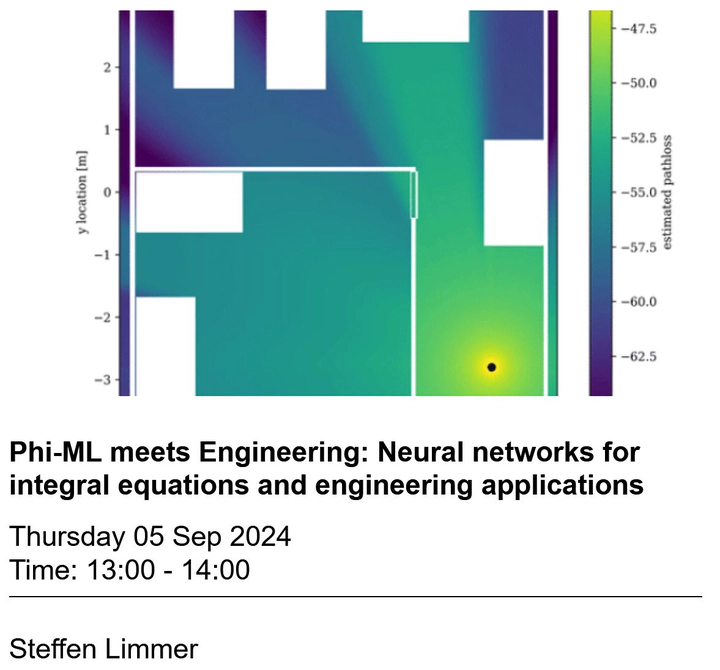
In this talk, we will explore different approaches that leverage neural networks for solving integral equations that appear in engineering applications. First, we introduce a physics-informed neural network for the problem of calculating line integrals in pathloss prediction. The method provides physically consistent pathloss estimates, while offering fast inference times and automatic differentiation useful for downstream tasks such as localization and network planning. Second, we introduce an approach to decompose neural networks into lower-dimensional models using the ANOVA decomposition. This Neural-ANOVA decomposition builds on closed-form integration over subspaces and enables an analysis of all learned interaction effects. Lastly, we discuss the application of Laplace techniques for designing neural networks to solve integrals over a particular class of polytopes that are given as the intersection of the simplex and an affine subspace. We show that classical deep neural networks with specialized activation functions can be designed to solve this problem in closed-form without training. These approaches collectively demonstrate the potential of neural networks for integral equations and advancing engineering applications through tailored network architectures and training methods.

Sep 5, 2024 12:00 AM